いもす金融理論

2020年2月21日公開

いもす金融理論

今まで正統派の金融理論の知識がある人との接触がなかったために、自分の金融理論の方向性が違うのを感じたため、この記事ではその根本部分の理論について金融理論を知らない人と正統派の金融理論を理解している人の両者に理解できるように説明を行い整理をします。
この記事は簡単に概要が理解できるようにしつつも論理の飛躍を抑えるため「青い破線」で示している箇所をクリックするとより詳細な説明が現れるようになっています。
青い破線で表されている箇所では、金融理論を知らない人向けにより一般的な言葉で説明を行ったり、仮定や式変形についてより詳細な説明を行っています。

0. はじめに: いもす金融理論と正統派金融理論との違い

いもす金融理論では、「すべての投資家にとって同一の答えとなる最適なポートフォリオの組成比」と「基準となる投資量」を同時に導くことを可能にします。資本資産価格モデル (CAPM) に従うのであれば、すべての投資家にとって最適ポートフォリオの組成比は同一であるはずです。しかし、正統派金融理論では投資できる量を資産と同一として制約をかけることが多く、効率的フロンティア上で様々な組成比の最適ポートフォリオが存在するかのように議論されることがあります。現代においてはレバレッジ商品を買うことは難しくないため、この制約は余分な制約です。また、現代ポートフォリオ理論では、投資家は自分の取りたいリスクや必要な利益の絶対量を決定するとすることが多いですが、現実には高い利益が得られるならより高いリスクを取りたいと思うのが自然なはずです。いもす金融理論では、分布を伴う投資の評価関数（効用関数）に対数関数を導入しその上ですべての議論を行うことで、これらの問題を解決します。
いもす金融理論は、金融理論に全くない理論というわけではありませんが、正統派とは異なり個人の投資戦略を最適化することを目的にしており、自己資産が有限であり戦略によって大きく変動することを前提としているため、議論の行い方が異なります。大きくわけると、以下の 2 点が異なります。
  • 分布を伴う投資の評価関数 U(x) （金融理論の言葉でいうと効用関数）として {\rm ln}(x) こそを用い、これの期待値を最大化するべきだと考えています。ポートフォリオ最適化を行う場合、正統派では期待利益（あるいは変動率）を固定してその中で変動率の最小化（あるいは期待利益の最大化）を行うことが多い（例: 現代ポートフォリオ理論 - Wikipedia）ですが、投資家は実際にはそれらを固定するのではなく割に合うリスクを取るべきとの思想から、最適化すべきものはリスクに対する期待利益の大きさと考えています。金融理論においてもリスク回避的な効用関数やシャープ・レシオなどを用いることがで、リスクに対する期待利益の大きさを最適化することがありますが、それらの中でも性質の良さから対数型効用関数こそを用いるべきと考えています。
  • 金融商品の持ち方は、自己資産に対する各金融商品の割合（レバレッジ）を固定するべきと考えています。正統派金融理論では、金融商品の量を自己資産で制限するか何かを制限した上で無限に借り入れられることを前提とし、短期間では金融商品の量を変えないことを想定することが多いですが、現実では証拠金・信用取引で上限レバレッジまで取引できることやリバランスを含む長期間について十分な表現ができないなどの問題があると考え、リバランスを含め連続時間で表現できる取引モデルとして「自己資産に対する各金融商品の割合（レバレッジ）を固定するべき」との立場を取っています。
この記事では効用関数を自己資産の評価関数として使います。例えば「50% の確率で資産が半分に、50% の確率で資産が 2 倍になる賭け」と「確実に資産が 1.1 倍になる賭け」のどちらが好ましいかは人によって異なります。これはその人の効用関数によって決まりと言い換えることができます。この例の場合、期待値（効用関数として線形関数を用いた場合、つまり U(x)=x のとき）は前者が後者より評価が高くなります U(0.5)×50%+U(2)×50% \gt U(1.1) が、効用関数として対数関数 U(x)={\rm ln}(x) を用いた場合は U(0.5)×50%+U(2)×50% \lt U(1.1) となり後者の方が評価が高くなります。
これらの前提を置くことで、自己資産を制限するモデルの下ではレバレッジ商品という現実にある金融商品を好んで買ってしまう傾向にある（逆に内部留保率が高く変動率が小さい株を過小に評価する）問題から為替オーバーレイ商品があまり評価されていない問題などまで様々なことが解決できると考えています。
この記事ではこれらについて数式を用いて説明を行います。1 章では、期待利益率および変動率のわかる金融商品が存在したときに対数期待効用のもとで最適レバレッジが決定できるようになることについて説明します。2 章では、ドル円などの安定した通貨間の為替において 1/2 倍レバレッジが対数期待効用を最大化するという結論が導き出されることについて説明します。

1. 金融モデル

この章では、いもす金融理論で用いる金融モデルを説明します。はじめに金融商品の価格変動モデルを紹介し、次にレバレッジをかけたときの資産変化についての説明を行います。

1.1. 金融商品の価格変動モデル

いもす金融理論では計算を簡単にするため無リスク金利はゼロとした上で、ブラック・ショールズ方程式に準じた価格変動モデルを用います。
無リスク金利が存在する場合、すべての人は現金を持たず無リスク金利のついた金融商品に置き換えることが有利であることから、無リスク金利のついた金融商品を元手に取引を行い無リスク金利のついた金融商品を基準にした価格を用いることが、リスクがないのに期待利益が減少する現金との比較を行うのと比べ、議論をよりシンプルにできると考えられます。また金融資産の一部を現金として持つような人、つまりリスクがないのに期待利益を捨てるような人が現れた場合、完全市場を仮定したときの矛盾が発生してしまうため、無リスク金利が 0 であると仮定した方がより式の上での矛盾が発生しにくいと考えられます。

1.1.1. 金融商品の価格変動モデル

時刻 t における金融商品の価格 S_t の変動を金融理論でよく用いられるブラック・ショールズ方程式を用いて表現します。単位時間あたりの変動率 σ および単位時間の期待利益 μ、ブラウン運動（ウィーナー過程） B_t を用いて以下のように変動すると定義します。
\[ \begin{eqnarray} dS_t & = & μS_tdt + σS_tdB_t \end{eqnarray} \]
これは微小時間 Δt の変動として以下のように定義することと同義です。
\[ \begin{eqnarray} S_{t+Δt} & = & \begin{cases} S_t (1 + μΔt + σ\sqrt{Δt}) & \cdots & 50\% \\ S_t (1 + μΔt - σ\sqrt{Δt}) & \cdots & 50\% \\ \end{cases} \end{eqnarray} \]

1.1.2. 金融商品の価格変動連続モデル

式 (1.1.1a) の確率微分方程式は伊藤の公式をもちいて、次のように式変形できます（参考: 幾何ブラウン運動 - Wikipedia）。
\[ d \ln(S_t) = \left( μ - \frac{σ^2}{2} \right) dt + σd B_t \]
時刻 t における金融商品の価格 S_t は、上式を積分し対数関数を展開することで以下のように求まります。
\[ S_t = S_0 \exp \left( \left(μ - \frac{σ^2}{2} \right)t + σ B_t \right) \]
上式は対数正規分布 {\rm Λ}(μ,μ^2σ^2)=μ\exp({\rm N}(0,σ^2)) の形で表現できることから、1.1 節の前提条件を満たす金融商品の価格は対数正規分布に従うことが示せます。
\[ S_t = S_0 \exp \left( \left(μ - \frac{σ^2}{2} \right)t \right) \exp(\mathcal{N}(0, tσ^2)) \]

1.1.3. 金融商品の価格の期待値と分散

この後の議論のベースとなるので、ブラック・ショールズ方程式に従って変動する金融商品の価格 S およびその対数について、期待値 {\rm E}[･] および分散 {\rm Var}[･] を求めます。
価格の期待値 {\rm E}[S_t] は、式 (1.1.2c) および対数正規分布の平均値を用いて以下のように求まります。
対数正規分布の平均値は以下のように表せます（参考: 対数正規分布 - Wikipedia）。 \[ {\rm E}[\exp(\mathcal{N}(0, σ^2))] = \exp(\frac{σ^2}{2}) \] 価格の期待値 {\rm E}[S_t] は、上式と式 (1.1.2c) を用いて以下のように求まります。 \[ \begin{eqnarray} {\rm E}[S_t] & = & {\rm E}[S_0] \exp \left( \left(μ - \frac{σ^2}{2} \right)t \right) \exp(\mathcal{N}(0, tσ^2)) \\ & = & {\rm E}[S_0] \exp \left( \left(μ - \frac{σ^2}{2} \right)t \right) \exp(\frac{tσ^2}{2}) \\ & = & {\rm E}[S_0] \exp(μt) \end{eqnarray} \]
\[ {\rm E}[S_t] = {\rm E}[S_0]\exp(μt) \]
価格の対数の期待値 {\rm E}[{\rm ln}(S_t)] は、式 (1.1.2b) およびブラウン運動の期待値 {\rm E}[σB_t] = 0 であることを用いて以下のように求まります。
\[ {\rm E}[\ln(S_t)] = {\rm E}[\ln(S_0)]+\left(μ - \frac{σ^2}{2} \right)t \]
価格の分散 {\rm Var}[S_t] は、まず {\rm E}[S_t^2] を式 (1.1.2b) を用いて計算し、分散は {\rm Var}[S_t] = {\rm E}[S_t^2] - ({\rm E}[S_t])^2 であることから、以下のように求まります。
具体的には、{\rm E}[S_t^2] は式 (1.1.2b) を用いて、式 (1.1.2b) が式 (1.1.3a) に式変形できるのと同様にブラウン運動の指数関数を展開すると、以下のように求まります。 \[ \begin{eqnarray} {\rm E}[S_t^2] & = & {\rm E}\left[ S_0^2 \exp \left( 2\left(μ - \frac{σ^2}{2} \right)t + 2σ B_t \right) \right] \\ & = & {\rm E}[S_0^2](1+(2μ+σ^2)t) \end{eqnarray} \] これと、分散 {\rm Var}[S_t] = {\rm E}[S_t^2] - ({\rm E}[S_t])^2　であることを用いて、価格の分散 {\rm Var}[S_t] は以下のように求まります。 \[ \begin{eqnarray} {\rm Var}[S_t] & = & {\rm E}[S_t^2] - ({\rm E}[S_t])^2 \\ & = & S_0^2(1+(2μ+σ^2)t) - (S_0(1+μt))^2 \\ & = & S_0^2(σ^2t-μ^2t^2) \end{eqnarray} \]
\[ {\rm Var}[S_t] = S_0^2(σ^2t-μ^2t^2) \]
価格の対数の分散 {\rm Var}[{\rm ln}(S_t)] は、式 (1.1.2b) を用いて以下のように求まります。
具体的には、式 (1.1.2b) を用いて式を展開すると、ブラウン運動に定数をかけても 0 であることから、ブラウン運動の 2 乗の項のみが残り、以下のように求まります。 \[ \begin{eqnarray} {\rm Var}[\ln(S_t)] & = & {\rm E}[\ln(S_t)^2] - ({\rm E}[\ln(S_t)])^2 \\ & = & \left( \begin{aligned} {\rm E}\left[\left( \ln(S_0)+\left(μ - \frac{σ^2}{2} \right)t + σ B_t \right)^2 \right] \\ - \left( {\rm E}[\ln(S_0)]+\left(μ - \frac{σ^2}{2} \right)t \right)^2 \\ \end{aligned} \right) \\ & = & {\rm E}[(σB_t)^2] \\ & = & σ^2t \end{eqnarray} \]
\[ \begin{eqnarray} {\rm Var}[{\rm ln}(S_t)] & = & σ^2t \end{eqnarray} \]

1.2. 金融取引のモデル: 有限な資産の上でレバレッジをかけるモデル

いもす金融理論では、有限な資産の上でレバレッジをかけられるようなモデルを用います。具体的には自分の金融資産の評価額に対して一定倍率（上限レバレッジ）をかけた金額までの借り入れができるというものです。これは、為替取引や先物取引などの証拠金取引と同様の仕組みです。正統派の金融理論では、「借り入れができない」あるいは「借り入れに制限のない」モデルを利用することが多いですが、これは借り入れ期間を超える長期での取引が表現できず、理論的にも離散的になってしまい不十分であると考えています。

1.2.1. レバレッジをかけたときの資産変動モデル

金融商品 S に対してレバレッジを L 倍かけたとき資産 V の変動は、変動量に対してレバレッジをかけることになることから、以下のようになります。
レバレッジを L 倍かけるとは、金融商品 S を VL/S 単位だけ買うということに相当します。金融商品の 1 単位の価格にかかわらず買い入れる金額が決定するため、資産に対しての期待利益率 μ_V=Lμ となり変動率 σ_V=Lσ となります。

証拠金取引の場合は仕組み上借り入れの必要はありませんが、現物取引や信用取引の場合には L \gt 1 とき V(L-1) の現金が不足するため、これは借り入れで対処しているとします。
\[ dV_t = LμV_tdt + LσV_tdB_t \]
これは式 (1.1.1a) に対して μ ← Lμ,\ σ ← Lσ を代入したときと一致することから、式 (1.1.2b) を用いて、資産 V は以下のように求まります。
\[ V_t = V_0 \exp \left( \left(Lμ - \frac{L^2σ^2}{2} \right)t + Lσ B_t \right) \]
これも式 (1.1.2c) と同様に、対数正規分布 {\rm Λ}(μ,μ^2σ^2)=μ\exp({\rm N}(0,σ^2)) の形で表現できることから、レバレッジをかけた場合の資産も対数正規分布に従うことが示せます。
\[ V_t = V_0 \exp \left( \left(Lμ - \frac{L^2σ^2}{2} \right)t \right) \exp(\mathcal{N}(0, tL^2σ^2)) \]

1.2.2. レバレッジをかけたときの資産の期待値と分散

式 (1.2.1b) を求めたのと同様に、式 (1.1.3a) および式 (1.1.3b)、式 (1.1.3c)、式 (1.1.3d) に対して μ ← Lμ,\ σ ← Lσ を代入することで、レバレッジをかけたときの資産およびその対数の期待値と分散が以下のように求まります。
\[ {\rm E}[V_t] = {\rm E}[V_0]\exp(Lμt) \]
\[ {\rm E}[\ln(V_t)] = {\rm E}[\ln(V_0)]+\left(Lμ - \frac{L^2σ^2}{2} \right)t \]
\[ {\rm Var}[V_t] = V_0^2L^2(σ^2t-μ^2t^2) \]
\[ {\rm Var}[{\rm ln}(V_t)] = L^2σ^2t \]

1.2.3. レバレッジによる中央値の減価

高いレバレッジをかけた金融商品は減価すると言われる所以を説明します。現実の金融商品はブラック・ショールズ方程式よりも短期的な変動幅が大きくより減価しやすいという問題はありますが、そうでなくともレバレッジをかけると中央値が減価するため、現実の世界ではレバレッジ商品の減価がよく観測されると考えられます。式 (1.2.1c) を用いて中央値を求めると以下のようになります。
\[ {\rm Median}[V_t] = V_0 \exp \left( \left(Lμ - \frac{L^2σ^2}{2} \right)t \right) \]
この式より中央値は最適レバレッジ L^*=μ/σ^2 を中心とした上に凸な二次関数となることがわかります。具体的に為替を模して μ=1%,\ σ=14% としたときの期待値と中央値のレバレッジとそのリターンをグラフにすると以下のようになります。
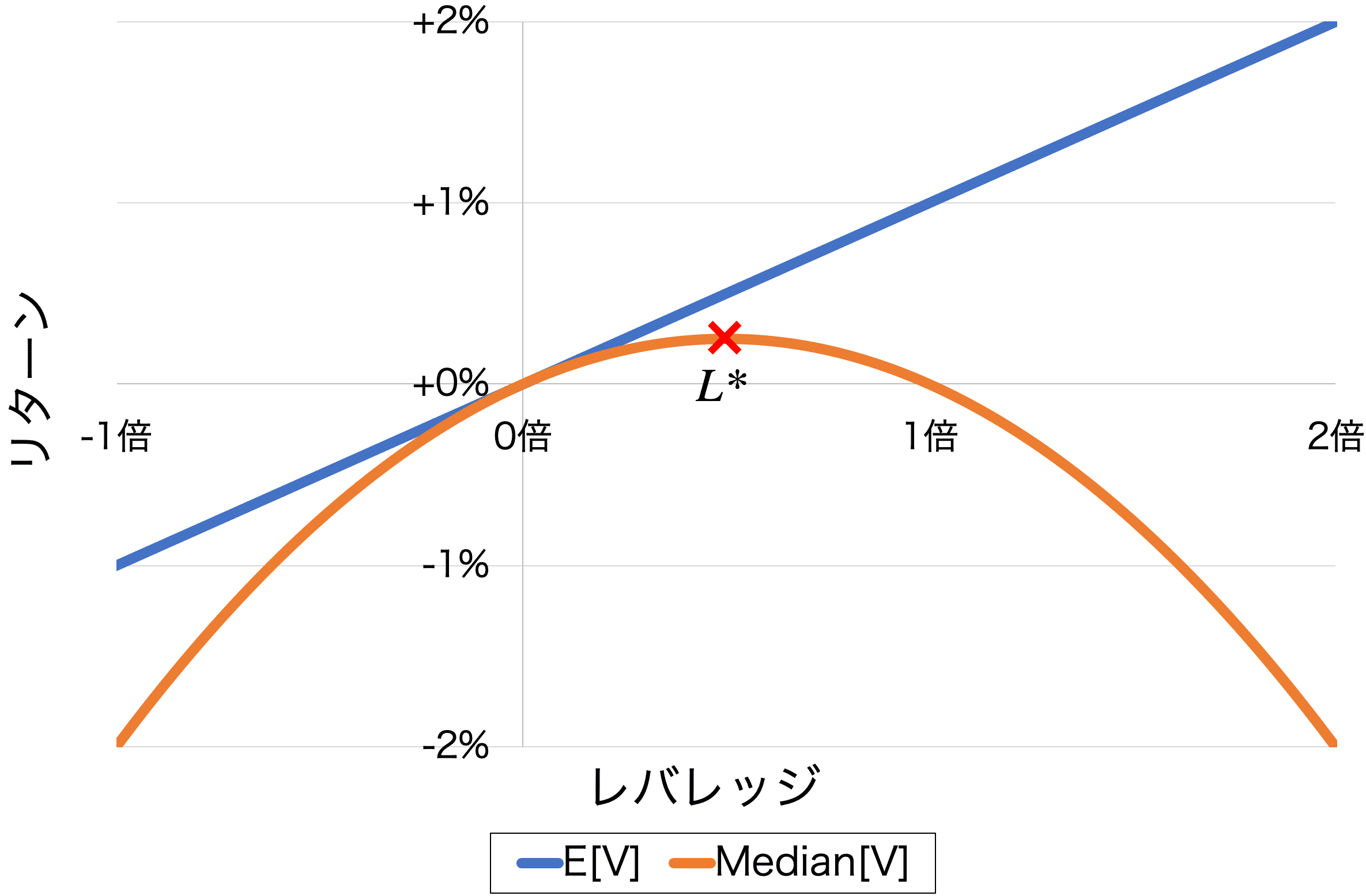
図 1.2.3: 期待値と中央値のレバレッジとリターンの関係
上図よりレバレッジをかければかけるほど中央値のリターンが期待値のリターンと乖離することがわかり、レバレッジ商品の減価を観測することになると考えられます。

1.2.4. 対数型効用関数を用いる理由

1.2.3 項で示したとおり、レバレッジを無限にかけると多くの場合でリターンが減少することから、それぞれの金融商品に対して何かしらの最適レバレッジがあると考えられます。そこで期待値 {\rm E}[･] やシャープレシオ {\rm SR}[･] などから最適レバレッジ L^* を計算します。
リスク中立な効用関数 U(x)=x を用いると、期待値およびシャープレシオは以下のように値が不定になるため、最適レバレッジの計算には使えません。
\[ \displaystyle\arg\max_L[{\rm E}[V_t]] = \infty \]
\[ \begin{eqnarray} \displaystyle\arg\max_L[{\rm E}[{\rm SR}[V_t]]] & = & \arg\max_L\left[\frac{{\rm E}[V_0]\exp(Lμt)}{\sqrt{V_0^2L^2(σ^2t-μ^2t^2)}}\right] \\ & = & \begin{cases} \infty & (μ > 0)\\ -\infty & (μ < 0) \end{cases} \end{eqnarray} \]
リスク回避的な効用関数として対数型効用関数 U(x)={\rm ln}(x) を用いると、期待値およびシャープレシオは以下のように求まります。
\[ \displaystyle\arg\max_L[{\rm E}[\ln(V_t)]] = \frac{μ}{σ^2} \]
\[ \begin{eqnarray} \displaystyle\arg\max_L[{\rm E}[{\rm SR}[\ln(V_t)]]] & = & \arg\max_L\left[\frac{\left(Lμ - \frac{L^2σ^2}{2} \right)t}{\sqrt{L^2σ^2t}}\right] \\ & = & \frac{2μ}{σ^2} \end{eqnarray} \]
リスク回避的な効用関数を用いた場合には、式 (1.2.4c) や式 (1.2.4d) のように、最適なレバレッジが μ/σ^2 に比例する値として決定できます。比例定数は効用関数によって異なりますがポートフォリオを構成する計算には影響を及ぼさないため、計算の簡単さや 1.2.3 節で示した中央値の最適レバレッジと一致する、ケリー基準から導き出される答えと一致するなどの性質の良さを考えて、いもす金融理論では対数型効用関数 U(x)={\rm ln}(x) を用います。
一貫したポートフォリオを構成できるリスク回避的な効用関数において最適なレバレッジが計算できる関数は、レバレッジを N 倍すると（μ を N 倍して、σ を N 倍したときに） 1/N 倍されることと、単位時間が T 倍すると（μ を T 倍して、σ を \sqrt{T} 倍したときに）変わらないことを満たす必要があります。そのような関数は、μ/σ^2 に比例する関数となります。

2. ポートフォリオ最適化

いもす金融理論では対数型効用関数を用います。そこで対数効用の上での最適ポートフォリオの計算方法を説明します。

3.1. 無相関な 2 つの銘柄によるポートフォリオ最適化

相関のない 2 つの銘柄でポートフォリオを構成したときの変動について考えます。式 (1.2.1a) より銘柄 A と銘柄 B を用いてポートフォリオを構成したときの変動は以下のように表せます。
\[ \displaystyle \begin{eqnarray} dV_t & = & \sum_{i \in \{{\rm A},\ {\rm B}\}} (L_iμ_idt + L_iσ_idB_{i,t}) \\ & = & \left( \sum_{i \in \{{\rm A},\ {\rm B}\}} L_iμ_i \right) dt + \sqrt{ \sum_{i \in \{{\rm A},\ {\rm B}\}} L_i^2σ_i^2 }dB_{t} \end{eqnarray} \]
次にポートフォリオを最適化するため対数期待効用を用いて評価を行います。式 (1.1.3b) を用いると以下のように求められます。
\[ {\rm E}[\ln(V_t)] = {\rm E}[\ln(V_0)] + \sum_{i \in \{{\rm A},\ {\rm B}\}} \left( L_iμ_i - \frac{(L_iσ_i)^2}{2} \right)t \]
上式を最大化する各レバレッジ L_{\rm A},\ L_{\rm B} を求めると以下のように求められます。
\[ \begin{aligned} L_i^* = \frac{μ_i}{σ_i^2} & & (i \in \{{\rm A},\ {\rm B}\}) \end{aligned} \]
以上より、相関のない銘柄を新たに取引するとき、すでに他の金融商品を買っているかと関係なく最適レバレッジが決まることがわかります。

2.2. 相関のある複数の銘柄によるポートフォリオ最適化

相関のある複数の銘柄でポートフォリオベクトル L を構成したときの変動について考えます。共分散行列 Σ を用いてポートフォリオを構成したときの変動は以下のように式 (2.1a) と同様の形で表せます。
共分散行列 Σ は以下のような性質を満たします（参考: 分散共分散行列 - Wikipedia）。 \[ \begin{eqnarray} & \textbf{Σ} = E \left[ (\textbf{X}-\textrm{E}[\textbf{X}]) (\textbf{X}-\textrm{E}[\textbf{X}])^\top \right] & \\ & \Downarrow & \\ & \textbf{Σ} = \textrm{E}[\textbf{XX}^\top] - \textrm{E}[\textbf{X}]\textrm{E}[\textbf{X}]^\top & \end{eqnarray} \] 次にブラウン運動ベクトル B_t の要素間の相関関係を、要素間が独立なブラウン運動 B_{\rm I, t} を用いて表現できる行列 M を以下のように定義します。 \[ d\textbf{B}_t = \textbf{M} d\textbf{B}_{\rm I, t} \] 上の 2 つの式より行列 M は共分散行列 Σ を用いて以下のように表わせます。 \[ \begin{eqnarray} \textbf{Σ} & = & \textrm{E}[(\textbf{σ}^\top d\textbf{B}_t)(\textbf{σ}^\top d\textbf{B}_t)^\top] \\ & = & \textrm{E}[\textbf{σ}^\top \textbf{M} d\textbf{B}_{\textrm{I}, t} d\textbf{B}_{\textrm{I}, t}^\top \textbf{M}^\top \textbf{σ}] \\ & = & \textbf{σ}^\top \textbf{M} \textbf{M}^\top \textbf{σ} \end{eqnarray} \] このことより資産 V_t の分散は以下のように求まります。 \[ \begin{eqnarray} \mathrm{Var}((\textbf{L} \circ \textbf{σ})^\top d\textbf{B}_t) & = & \textrm{E}[(\textbf{L} \circ \textbf{σ})^\top d\textbf{B}_t d\textbf{B}_t^\top (\textbf{L} \circ \textbf{σ})] \\ & = & \textbf{L}^\top (\textbf{σ}^\top \textbf{M} (\textrm{E}[d\textbf{B}_{\textrm{I}, t} d\textbf{B}_{\textrm{I}, t}^\top]) \textbf{M}^\top \textbf{σ}) \textbf{L} \\ & = & \textbf{L}^\top \textbf{Σ} \textbf{L} \end{eqnarray} \]
\[ \begin{eqnarray} dV_t & = & \textbf{μ}^\top\textbf{L} + \textbf{σ}d\textbf{B}_t\\ & = & \textbf{μ}^\top \textbf{L} + \sqrt{\textbf{L}^\top \textbf{Σ} \textbf{L}}dB_t \end{eqnarray} \]
次にポートフォリオを最適化するため対数期待効用を用いて評価を行います。式 (1.1.3b) を用いると以下のように求められます。
\[ {\rm E}[\ln(V_t)] = {\rm E}[\ln(V_0)] + \textbf{L}^\top \textbf{μ} - \frac{\textbf{L}^\top \textbf{Σ} \textbf{L}}{2} \]
上式を最大化するポートフォリオ L^* を求めると以下のように求められます。
最適ポートフォリオ L^* は、式 (2.2b) から以下の式を最大化するポートフォリオ L と定義できます。 \[ \textbf{L}^* = \arg\max_\textbf{L}\left( \textbf{μ}^\top \textbf{L} - \frac{\textbf{L}^\top \textbf{Σ} \textbf{L}}{2} \right) \] 共分散行列は非負行列であることから上式は上に凸な二次関数であり、上式の右辺 argmax 内の微分値が 0 ベクトルになるときに最大化されることがわかります。そこで上式の argmax 内の式を L で微分したものは以下のように求められます。 \[ \begin{eqnarray} 0 & = & \frac{\partial}{\partial L} \left( μ^\top L - \frac{L^\top Σ L}{2} \right) \\ & = & μ - Σ L \end{eqnarray} \] よって最適ポートフォリオ L^* は以下のように求まります。 \[ L^* = Σ^{-1} μ \]
\[ \begin{eqnarray} \textbf{L}^* & = & \arg\max_\textbf{L}\left( \textbf{μ}^\top \textbf{L} - \frac{\textbf{L}^\top \textbf{Σ} \textbf{L}}{2} \right) \\ & = & \textbf{Σ}^{-1} \textbf{μ} \end{eqnarray} \]
以上より、各銘柄の変動が線形独立であるとき（共分散行列の逆行列が求められるとき）相関のある複数の銘柄に対する最適レバレッジが決まることがわかります。

3. 為替の変動モデル

いもす金融理論では為替を、為替は流動性が非常に高く非常に理想的な変動を行うことから、特別に重要な金融商品として扱います。

3.1. 為替の変動モデル

為替、特にドル・ユーロ・円などの市場が非常に大きな通貨間の変動は理想的であるため、金利差について打ち消したときの微小時間 Δt の変動は以下のように表現できます。
\[ \begin{eqnarray} S_{t+Δt} & = & \begin{cases} S_t (1 + σ\sqrt{Δt}) & \cdots & 50\% \\ S_t \frac{1}{1 + σ\sqrt{Δt}} & \cdots & 50\% \\ \end{cases} \end{eqnarray} \]
十分に実需が大きく流動性の高い 2 つの通貨 A, B を考えます。それぞれの国の人がもう一方の通貨を買い、\exp(d) 倍になり利益確定されるか \exp(-d) 倍になり損切りされるという OCO 注文を行うとします。
  • 通貨 A が通貨 B に対して \exp(d) 倍になったとき、A 国の人の注文は \exp(d) 倍になり利益確定され、B 国の人の注文は \exp(-d) 倍になり損切りされます。
  • 通貨 A が通貨 B に対して \exp(-d) 倍になったとき、A 国の人の注文は \exp(-d) 倍になり損切りされ、B 国の人の注文は \exp(d) 倍になり利益確定されます。
前者あるいは後者の確率が高いとすると通貨 A と通貨 B の変動が可換ではなくなり矛盾するため、それぞれの変動は同一であると考えられます。このことから為替変動は式 (1.1.1) の r=0 である状態で表現できると考えられます。
これを式 (1.1.1b) の形になるように式変形を行うと以下のようになります。
\[ \begin{eqnarray} S_{t+Δt} & = & \begin{cases} S_t (1 + \frac{σ^2}{2}Δt + σ\sqrt{Δt}) & \cdots & 50\% \\ S_t (1 + \frac{σ^2}{2}Δt - σ\sqrt{Δt}) & \cdots & 50\% \\ \end{cases} \end{eqnarray} \]
このことから為替の変動は 1 章で説明した金融商品の価格変動モデルを期待利益 μ=σ^2/2 とした状態で表せます（期待利益が 0 とならないことはシーゲルのパラドクスとして知られています）。この時の各効用関数での期待値を式 (1.2.2a) および式 (1.2.2b) を用いて計算すると以下のようになり、線形効用関数での最適レバレッジ L^*=∞、対数型効用関数での最適レバレッジ L^*=1/2 となります。
\[ {\rm E}[V_t] = {\rm E}[V_0]\exp(\frac{1}{2}Lσ^2t) \]
\[ {\rm E}[\ln(V_t)] = {\rm E}[\ln(V_0)]+\frac{1}{2}L(1-L)σ^2t \]

3.2. 真の価値の導入

真の価値というものが存在し各通貨は真の価値に対して期待利益 μ=0 の変動をしていると仮定すると、3 つ以上の通貨が存在する場合や変動率の異なる通貨が存在する場合の挙動がわかりやすくなるため、そのモデルについて紹介します。

3.2.1. 真の価値に対する通貨の変動

変動率 σ の通貨 A をレバレッジ L 倍で持ったときの真の価値に対する資産の価値 V_{{\rm true}, t} の変動は、期待利益 μ=0 の変動をしているという 3.2 節の仮定から、式 (1.2.2b) に代入することで以下のように求められます。
\[ \textrm{E}[d\ln(V_{{\rm true}, t})] = -\frac{L^2σ^2}{2}dt \]

3.2.2. 3 つ以上の通貨

自国通貨 S_t および N 個の外国通貨があり、それらが真の価値に対して変動率 σ で独立に変動しているとします。各外国通貨をレバレッジ L 倍で持ったとき、自国通貨のレバレッジは 1-NL 倍になることから、自国通貨に対する資産の価値 V_t は式 (3.2.1a) を用いて以下のように求められます。
\[ \begin{eqnarray} \textrm{E}[d\ln(V_t)] & = & \textrm{E}\left[ d\ln\left( \frac{V_{{\rm true}, t}}{S_{{\rm true}, t}} \right) \right]\\ & = & \textrm{E}[d\ln(V_{{\rm true}, t})] -\textrm{E}[d\ln(S_{{\rm true}, t})] \\ & = & -\frac{(1-NL)^2σ^2}{2}dt -\frac{NL^2σ^2}{2}dt +\frac{σ^2}{2}dt \\ & = & (1-(1-NL)^2-NL^2)\frac{σ^2}{2}dt \end{eqnarray} \]
上式を最大化するレバレッジ L^* は以下のように求められます。
\[ \begin{eqnarray} L^* & = & \arg\max_{L}(1-(1-NL)^2-NL^2) \\ & = & \arg\max_{L}(-(N^2+N)L^2+2NL) \\ & = & \frac{1}{N+1} \end{eqnarray} \]
上式より自国通貨を含めて各通貨を均等に持つことが、自国通貨に対する資産の価値 V_t の対数型効用関数を最大化する最適ポートフォリオとなります。

3.2.3. 変動率の異なる通貨

ここまではすべての通貨が同じ変動率であるという仮定が入っていました。そこで変動率の異なる通貨が存在するときの最適ポートフォリオを計算します。
真の価値に対する変動率 σ_{\rm self} の自国通貨および、変動率ベクトル σ の外国通貨群があります。これに対して外国通貨群をレバレッジベクトル L で持ったとき、自国通貨に対する資産の価値 V_t は式 (3.2.2a) と同様に以下のように求まります。
\[ \begin{eqnarray} \textrm{E}[d\ln(V_t)] & = & -\frac{(1-\displaystyle\sum_{i} \textbf{L}_i)^2σ_\textrm{self}^2}{2}dt -\frac{\displaystyle\sum_i \textbf{L}_i^2 \textbf{σ}_i^2}{2}dt +\frac{σ_\textrm{self}^2}{2}dt \end{eqnarray} \]
上式を最大化する最適ポートフォリオ L^* は以下のように求まります。
具体的には、上式が上に凸な関数であることから、偏微分が 0 となるレバレッジベクトル L を求めれば良いことがわかります。上式の偏微分を求めると以下のようになります。 \[ \begin{eqnarray} 0 & = & \frac{\partial}{\partial\textbf{L}_j}\textrm{E}[d\ln(V_t)] \\ & = & \left( 1 - \left( \displaystyle\sum_{i} \textbf{L}_i \right) \right) σ_\textrm{self}^2 - \textbf{L}_j \textbf{σ}_j^2 \end{eqnarray} \tag{3.2.3i} \] 上式を式変形すると以下の式が得られます。 \[ \textbf{L}_j=\frac{ \left( 1 - \left( \displaystyle\sum_{i} \textbf{L}_i \right) \right) σ_\textrm{self}^2 }{\textbf{σ}_j^2} \tag{3.2.3j} \] 上式の {\rm Σ} を展開するため、上式を用いて {\rm Σ} L_i を計算すると以下のようになります。 \[ \begin{eqnarray} \sum_i{\textbf{L}_i} & = & \left( 1 - \left( \displaystyle\sum_{i} \textbf{L}_i \right) \right) σ_\textrm{self}^2 \sum_i\frac{1}{\textbf{σ}_i^2} \\ & = & 1-\frac{1}{1+\displaystyle\sum_i\frac{σ_\textrm{self}^2}{\textbf{σ}_i^2}} \end{eqnarray} \tag{3.2.3k} \] 上式を式 (3.2.3j) に代入することで以下のように最適ポートフォリオ L^* が以下のように求まります。
\[ \textbf{L}_j^*=\frac{1}{\displaystyle\frac{1}{σ_\textrm{self}^2}+\sum_i\frac{1}{\textbf{σ}_i^2}}\frac{1}{\textbf{σ}_j^2} \]
真の価値に対する変動率が異なる通貨が存在するとき、変動率の逆数に比例した割合で投資すると良いことがわかります。 またこのことから 3.1 節や 3.2.2 項の結論は真の価値に対する分散が同じ通貨ペアでしか成立しないことがわかります。

4. 結論

  • 1.1.2 項で示したとおり、ブラック・ショールズ方程式を用いて表せる金融商品の価格は対数正規分布で表現できます。
  • 1.2.3 項で示したとおり、高いレバレッジをかけるとリターンの中央値が大きく減少します。
  • 1.2.4 項で示したとおり、いもす金融理論では対数型効用関数 U(x)={\rm ln}(x) を利用します。これは対数正規分布に従う金商品の価格について中央値を最大化する最適化していることと一致します。
  • 1.2.4 項で示したとおり、中央値を最大化する最適レバレッジ L^* は金融商品の価格 S を用いて以下のように求まります。
\[ L^* = \frac{μ}{σ^2} = \frac{\ln({\rm E}[S_t])-\ln(S_0)}{{\rm Var}[{\rm ln}(S_t)]} \]
  • 2.1 節で示したとおり、複数の独立した変動をする銘柄の最適ポートフォリオと各銘柄の最適レバレッジは一致します。
  • 2.2 節で示したとおり、相関のある複数の銘柄の最適ポートフォリオは期待利益ベクトル μ および共分散行列 Σ を用いて以下のように求まります。
\[ L^* = Σ^{-1} μ \]
  • 3.1 節で示したとおり、自国と同等に安定した 1 つの外国通貨のみが売買できる環境下で資産の対数期待効用を最大化したい場合には、レバレッジ 0.5 倍（資産評価額の半額を外国通貨）で持つことで実現できます。