いもす法

2012年12月23日公開

いもす法

いもす法とは，累積和のアルゴリズムを多次元，多次数に拡張したものです．競技プログラミングでは 2 次元 1 次のものまでしか出題されませんが，2012 年の研究成果としてこれをより高次元の空間により高次数のいもす法を適用することにより信号処理分野・画像処理分野において利便性があることがわかっています．

いもす法の基本: 1 次元 0 次いもす法

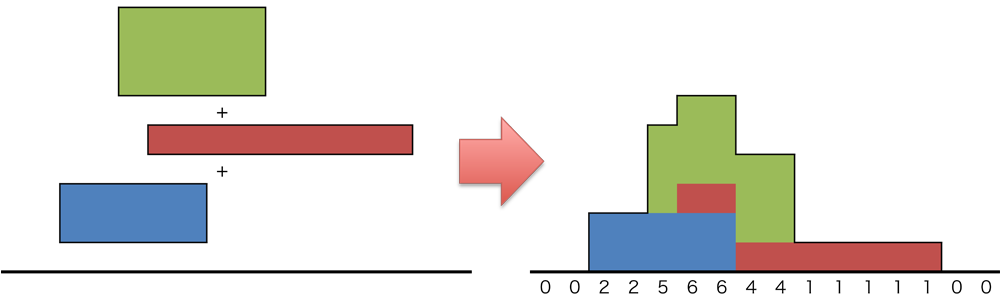
最もシンプルな「いもす法」は 1 次元上に 0 次関数（矩形関数や階段関数などのように上部が平らな関数）を足すものです．
図 1: 1 次元上へ 0 次関数を加算するイメージ

問題例

あなたは喫茶店を経営しています．あなたの喫茶店を訪れたそれぞれのお客さん i\ (0 \leq i \lt C) について入店時刻 S_i と出店時刻 E_i が与えられます（0 \leq S_i \lt E_i \leq T）．同時刻にお店にいた客の数の最大値 M はいくつでしょうか．ただし，同時刻に出店と入店がある場合は出店が先に行われるものとします．（また解法としては，C が非常に大きい場合でも O(C+T) の計算量で解けることが期待されているものとします．）

ナイーブな解法

ナイーブな解法としては，それぞれのお客さんについて滞在した各時刻のカウントを 1 足す方法が挙げられます．しかし，これの計算量は O(CT) です． 
for (int i = 0; i < T; i++) table[i] = 0;
for (int i = 0; i < C; i++) {
  // 時刻 S[i] から E[i] - 1 までのそれぞれについてカウントを 1 増やす
  for (int j = S[i]; j < E[i]; j++) {
    table[j]++;
  }
}
// 最大値を調べる
M = 0;
for (int i = 0; i < T; i++) {
  if (M < table[i]) M = table[i];
}

いもす法による解法

いもす法では，出入り口でのカウントのみをするという発想で入店時に +1 を，出店時に -1 を記録しておき，答えを求める直前に全体をシミュレートします．記録には O(C) が，シミュレートには O(T) がかかるので，全体としての計算量は O(C+T) となります． 
for (int i = 0; i < T; i++) table[i] = 0;
for (int i = 0; i < C; i++) {
  table[S[i]]++;  // 入店処理: カウントを 1 増やす
  table[E[i]]--;  // 出店処理: カウントを 1 減らす
}
// シミュレート
for (int i = 0; i < T; i++) {
  if (0 < i) table[i] += table[i - 1];
}
// 最大値を調べる
M = 0;
for (int i = 0; i < T; i++) {
  if (M < table[i]) M = table[i];
}

次元の拡張

いもす法の 1 番の特徴はナイーブな方法と比較して，次元の上昇に強いという点です．次元の呪いからは逃れられないので高次元に適用することは難しいですが，問題設定として 2 次元や 3 次元が用いられることは非常に多く，それらの状況においていもす法は有用です．

問題例

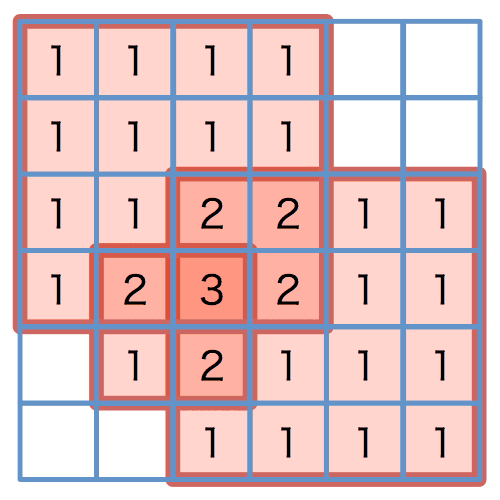
あなたは様々な種類のモンスターを捕まえるゲームをしています．今あなたがいるのは W\times H のタイルからなる草むらです．この草むらでは N 種類のモンスターが現れます．モンスター i は A_i ≦ x < B_i,\ C_i ≦ y < D_i の範囲にしか現れません．このゲームを効率的に進めるため，1 つのタイル上で現れるモンスターの種類の最大値が知りたいです．（ただし，W\times H は計算可能な程度の大きさとし，N は大きくなりうるものとします．）
図 2: モンスターが現れる矩形（赤色）と，
各タイルで現れるモンスターの種類の数

ナイーブな解法

ナイーブな解法としては，それぞれのモンスターについて現れる矩形の範囲に含まれるすべてのタイルについて 1 を足す方法が挙げられます．しかし，これの計算量は O(NWH) です． 
for (int y = 0; y < H; y++) {
  for (int x = 0; x < W; x++) {
    tiles[y][x] = 0;
  }
}
for (int i = 0; i < N; i++) {
  // モンスター i が現れる [(A[i],C[i]), (B[i],D[i])) の範囲に 1 を足す
  for (int y = C[i]; y < D[i]; y++) {
    for (int x = A[i]; x < B[i]; x++) {
      tiles[y][x]++;
    }
  }
}
// 最大値を調べる
int tile_max = 0;
for (int y = 0; y < H; y++) {
  for (int x = 0; x < W; x++) {
    if (tile_max < tiles[y][x]) {
      tile_max = tiles[y][x];
    }
  }
}

いもす法による解法

いもす法では，矩形の左上 (A[i],C[i]) に +1 を，右上 (A[i],D[i]) に -1 を，左下 (B[i],C[i]) に -1 を，右下 (B[i],D[i]) に +1 を加算し，答えを求める直前に累積和を求めます．記録には O(N) が，累積和の計算には O(WH) がかかるので，全体としての計算量は O(N+WH) となります． 
for (int y = 0; y < H; y++) {
  for (int x = 0; x < W; x++) {
    tiles[y][x] = 0;
  }
}
// 重みの加算 (図 3)
for (int i = 0; i < N; i++) {
  tiles[C[i]][A[i]]++;
  tiles[C[i]][B[i]]--;
  tiles[D[i]][A[i]]--;
  tiles[D[i]][B[i]]++;
}
// 横方向への累積和 (図 4, 5)
for (int y = 0; y < H; y++) {
  for (int x = 1; x < W; x++) {
    tiles[y][x] += tiles[y][x - 1];
  }
}
// 縦方向の累積和 (図 6, 7)
for (int y = 1; y < H; y++) {
  for (int x = 0; x < W; x++) {
    tiles[y][x] += tiles[y - 1][x];
  }
}
// 最大値を調べる
int tile_max = 0;
for (int y = 0; y < H; y++) {
  for (int x = 0; x < W; x++) {
    if (tile_max < tiles[y][x]) {
      tile_max = tiles[y][x];
    }
  }
}
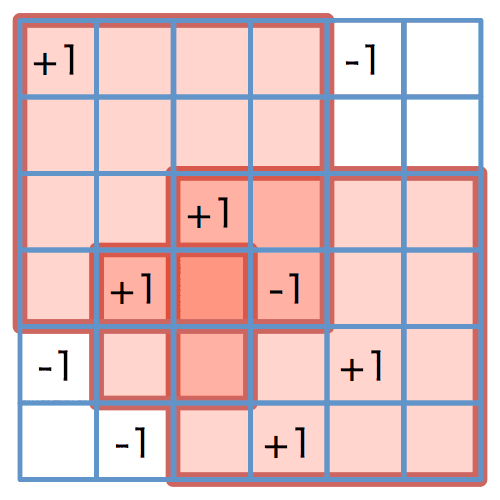
図 3: 重みの加算の結果
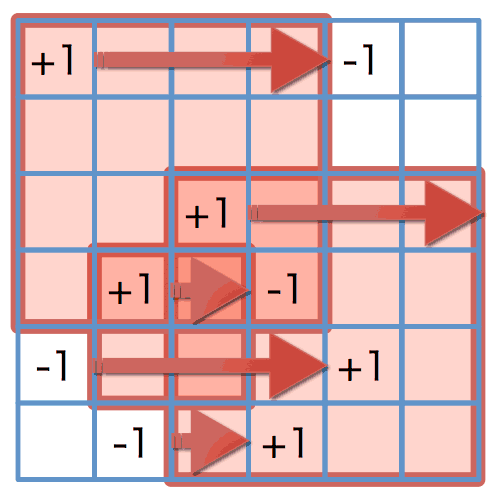
図 4: 横方向への累積
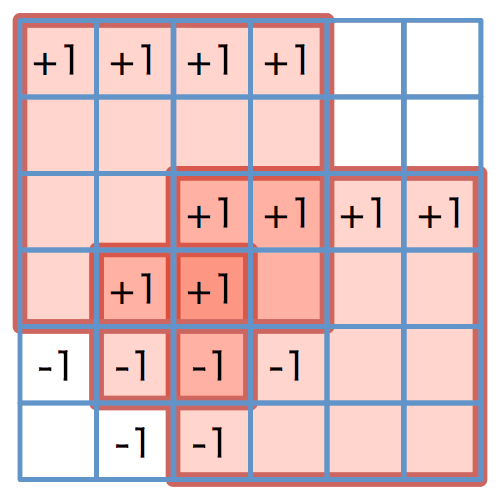
図 5: 横方向への累積の結果
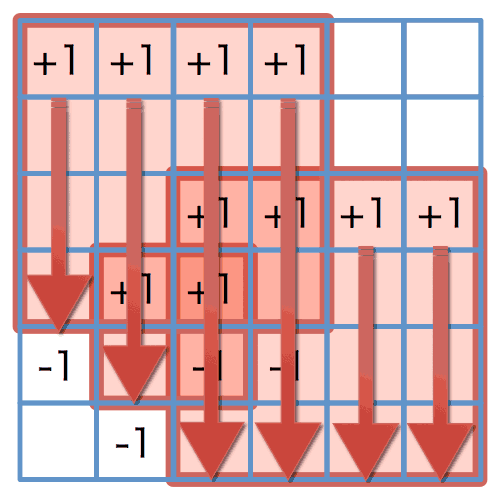
図 6: 縦方向への累積
図 7: 縦方向への累積の結果

特殊な座標系への拡張

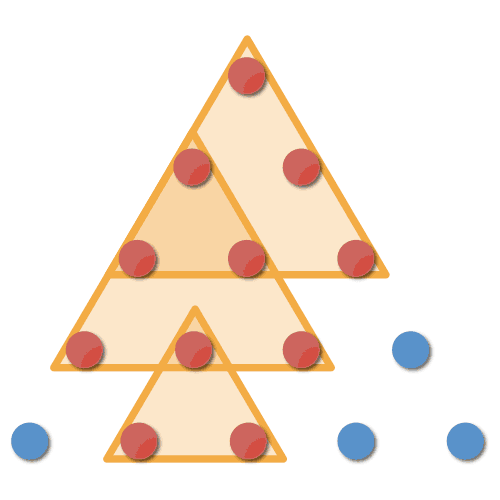
いもす法は三角形や六角形の座標系にも適用できます．どこに重みを加算して，どのような方向に累積するのかは，目標となる形に対してできる限り数が少なくなるような方向に様々な方向に差分を取って見つけます．
図 8: 三角形の座標系

差分を取る手法

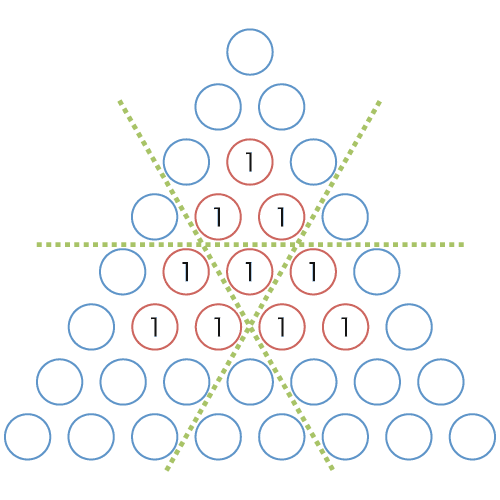
図 9 は三角形の座標系において埋めるべき重みを表しています．緑の線は間が省略されていることを示します（一辺の長さが 4 である三角形の場合には線を無視してもこれらの図では同様の結果になります）．いもす法でこのような重み付けを行うため，重みのあるセルの数が十分に少なくなるまで差分をとって，重みを付けるべきセルの配置と累積和をとる方向を知る必要があります．
図 9 〜 12 は差分をとる過程を表しています．これらの間に，「左上から右下への差分」「右上から左下への差分」「左から右への差分」をとったので，いもす法で三角形の累積和を求める場合は，図 12 のように数値を配置し逆の動作「左から右への累積和」「右上から左下への累積和」「左上から右下への累積和」を行います．
図 9: 埋めるべき重み
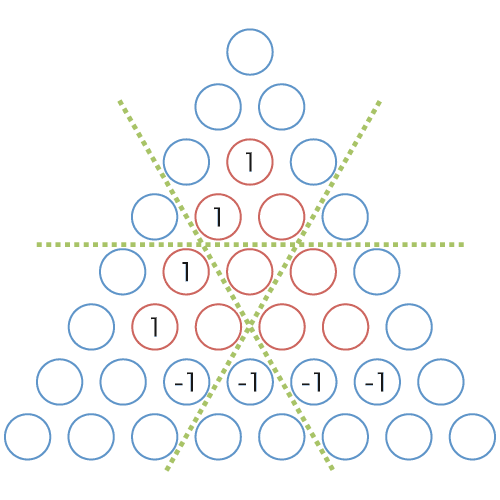
図 10: 図 9 の左上から右下への差分
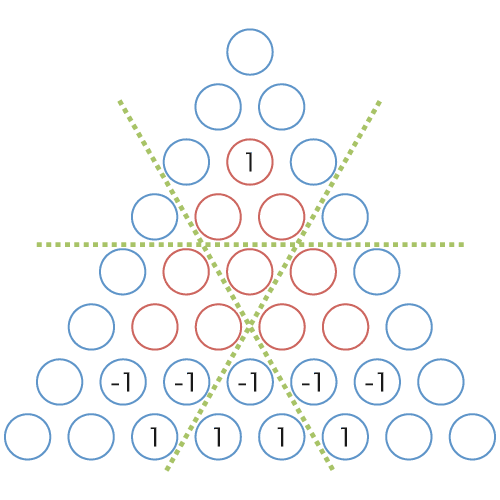
図 11: 図 10 の右上から左下への差分
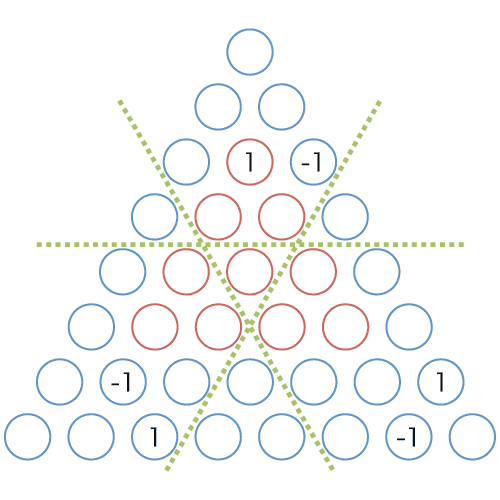
図 12: 図 11 の左から右への差分
同様の方法は三角形だけではなく，六角形の場合や，つける重みが定数ではなく傾き（ただし，多項式に限る）を持っている場合にも適用できます．

次数の拡張

競技プログラミングで出題される問題は高くとも 1 次までだとは思いますが，いもす法は高次の区分多項式関数も適用することができます．本来多項式で良い近似が得られないと思われている関数が区分多項式で表せられることがあり，それを利用すると連続ウェーブレット変換の高速化が可能になります．

2 次関数の差分

試しに 1 次元上で 2 次関数のいもす法を行なってみましょう．
01234 56789
00014 916253649
↓差分　　　↑累積和
01234 56789
00013 5791113
↓差分　　　↑累積和
01234 56789
00012 22222
↓差分　　　↑累積和
01234 56789
00011 00000
図 13: 2 次関数 (x-2)_+^2 の差分
図 13 より，2 次関数 (x-a)_+^2 を加算するとき，テーブルの a+1 および a+2 に 1 を加算し，最後に 3 度累積和をとることにより 2 次関数を用いた，いもす法が適用できることがわかります（ただし，(･)_+ = {\rm max}(0,･) とする）．同様の方法で，より高次の関数であっても，いもす法が適用可能です．

ガウス関数といもす法

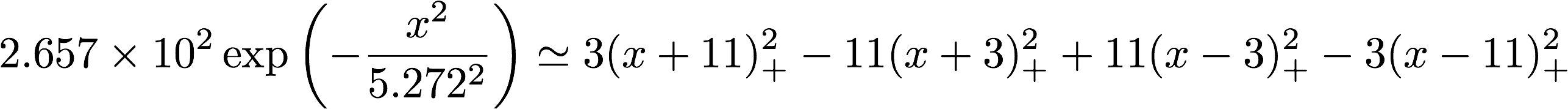
次数の拡張の例としてガウス関数を見てみましょう．いもす法を適用するため，式 1 の左辺に表されるようなガウス関数を，右辺のような区分多項式で近似します．この近似関数は図 14 に示されるように非常によく近似されています．
式 1: ガウス関数（左辺）とその近似（右辺）
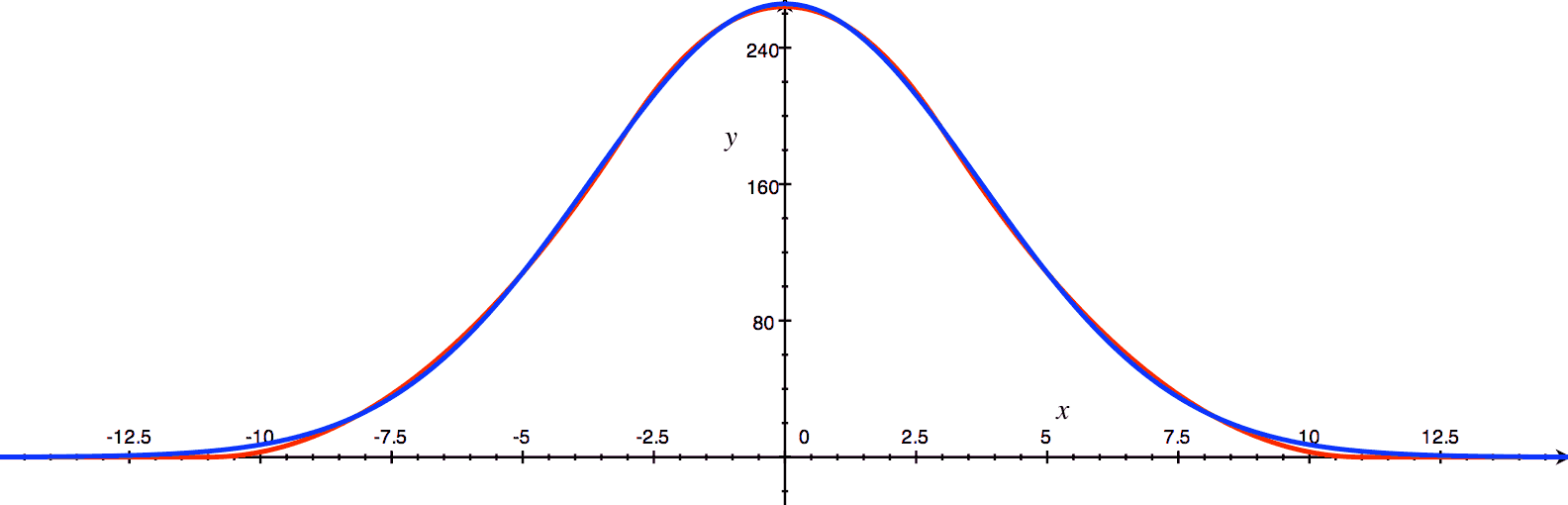
図 14: ガウス関数（青）と多項式近似（赤）
-12-11-10 -9-8-7-6-5 -4-3-2-10 12
003 30000 00-11-110 00
↓累積和　　　↑差分
-12-11-10 -9-8-7-6-5 -4-3-2-10 12
003 66666 66-5-16-16 -16-16
↓累積和　　　↑差分
-12-11-10 -9-8-7-6-5 -4-3-2-10 12
003 915212733 394540248 -8-24
↓累積和　　　↑差分
-12-11-10 -9-8-7-6-5 -4-3-2-10 12
003 12274875108 147192232256264 256232
図 15: いもす法によって近似されたガウス関数
-12-11-10 -9-8-7-6-5 -4-3-2-10 12
1
.49		3
.42		7
.28		 14
.41		26
.57		45
.58		72
.76		108
.08		 149
.41		192
.20		230
.09		256
.31		265
.70		 256
.31		230
.09
図 16: 近似目標となるガウス関数
さらに，d 次元のガウス関数は 1 次元のガウス関数の積で表すことができるので，d 次元のいもす法が適用できます．またガウス関数は，中心からのユークリッド距離で重みが決まる（2 次元上では円形，3 次元上では球形である）ため，回転不変な値をとりたい時などに非常に有用です．
これについてより詳しく知りたい場合は，ICPR 2012 での発表資料をご参照ください．

付録

いもす法が使える問題

  • [簡単] Osaki … 1 次元 0 次いもす法，ACM-ICPC Japan Alumni Group Practice Contest for Japan Domestic 2007 - [AOJ]
  • [簡単] 釘 (Nails) … 三角形座標の 0 次いもす法，日本情報オリンピック2012年 本選4番 - [AOJ]
  • [普通] ペンキの色 … 座標圧縮＋ 2 次元 0 次いもす法＋幅優先探索（スタックの容量次第では深さ優先探索も可），日本情報オリンピック2008年 本選5番 - [AOJ]
  • [普通] Plugs … 2 次元 0 次いもす法＋アドホック，日本情報オリンピック2010年 合宿4日目4番
  • [難] Pyramid … 特殊な座標系の 1 次いもす法，Autumn Fest 2012: I